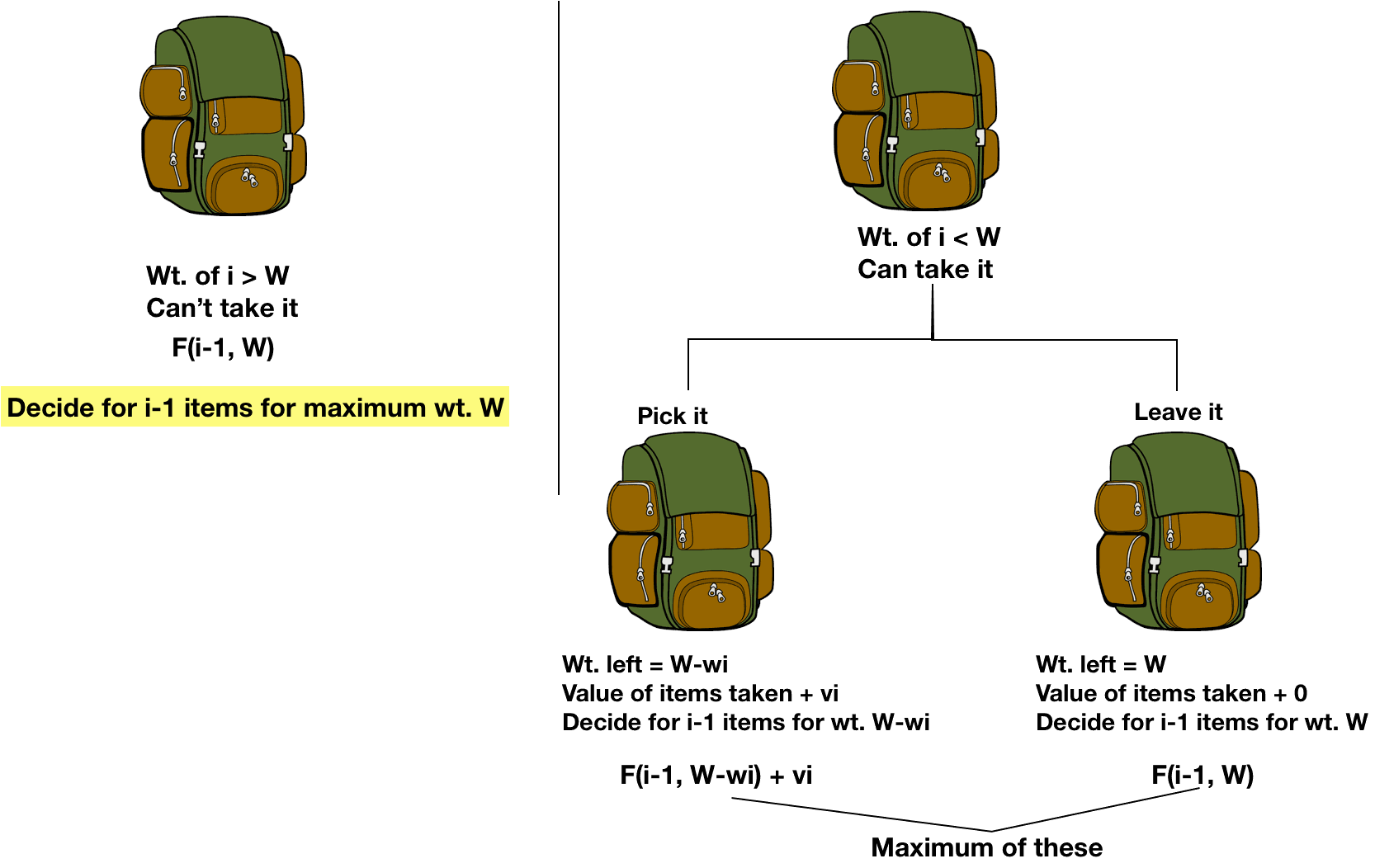
restrockstar.blogg.se - Knapsack problem

#KNAPSACK PROBLEM FULL#

Both approaches do not guarantee the optimal solution. If you look at this example, you might think that our second approach is good and will provide us with optimal results every time, but it is not. Now, the bag is completely filled, let us see the profit in this case-: When we load this object into the bag, our bag would be completely filled. Now the capacity of the bag is 5kg but the next minimum weight is ‘6’, therefore we will take 5 out of that 6 and the profit will be calculated accordingly. After loading this object, the bag is left with-: The second object with the minimum weight is the 4th object with weight ‘5’.The profit associated with this object is ‘15’. Therefore, after loading this object to the bag, the remaining bag capacity is-: The weight associated with 3rd object = 2 The first object with the minimum weight = 2nd object Selecting the solution with respect to the minimum weight.Now, let us calculate the profit while selecting the solutions on the basis of minimum weight.

#KNAPSACK PROBLEM FULL#

Now, the bag is completely full and we cannot add any more objects to the bag, we shall calculate the profit-: After loading this object to the bag, the capacity of the bag remains-: The next object with maximum profit is the 3rd object, where the profit is ‘14’ and the weight is ‘7’. Therefore, if we load this object to the bag we are left with = 12-5 = 7 The weight associated with the 4th object = 5 If we select maximum objects with the maximum profit to fill the bag, then the solution will be-:

Selecting the solution with respect to the maximum profit.

(Read blog: What Does Probabilistic Programming Work?) Now, what should be our approach to fill the bag? We can either choose the object with a maximum profit or maximum weight, let’s try out both approaches. We can see that the total weight of the objects is exceeding the capacity of the bag( total weight: 6 + 2 + 7 + 5 = 20). We can see in the above example that there are 4 objects and in the example, we can also see the profit and weights of the object. Now let us take objects, object weights, and profit associated with that weight. The weight of the objects should be less than or equal to the capacity of the bag.Ĭonsider a bag that has a capacity of 12 kg, let's take the maximum capacity of a bag as ‘m’, here m = 12. The constraint is to fill the objects such that the weight of the objects doesn’t exceed the capacity of a bag. As we are trying to maximize the profit, this problem is optimization as well as maximization problem.Įvery optimization problem has some sort of constraint associated with it, what is the constraint here? The knapsack examples help in real-world such as resource allocation problems.Ī knapsack can also be considered as a bag and the problem is to fill the bag with the objects in such a way that the profit is maximized.

The Knapsack problem is used in logistics, mathematics, cryptography, computer science, and more. The optimization problem needs to find an optimal solution and hence no exhaustive search approach could be applied to it. The knapsack problem is one of the famous and important problems that come under the greedy method.Īs this problem is solved using a greedy method, this problem is one of the optimization problems, more precisely a combinatorial optimization.